[itbase2021]gnuplot 実習
はじめに
gnuplot
gnuplot は数値データや数学関数のグラフをつくるソフトウェアです. 点と線を使った 2 次元グラフのだけでなく, メッシュや等高線を使った 3 次元グラフも描くことができます. gnuplot はフリー(無料)ソフトウェアです. ここでは Unix(Mac) 上で gnuplot を練習しますが, Windows 版の gnuplot もあり, 基本的な使い方は同じです. 気に入ったら自分の PC にインストールしてみて ください.
準備
さっそく起動してみたいところですが, そのまえに準備をしましょう. ターミナルを開いて Gnuplot というディレクトリを作り, そこに移動 しましょう. 今日はこのサブディレクトリで gnuplot の練習をすることにします.
istc c-012:~ 0123456s$ mkdir Gnuplot istc c-012:~ 0123456s$ cd Gnuplot
こうしておけば, 今日練習でつくった gnuplot 関係のファイルが ディレクトリにまとめられるのでファイルの整理整頓になります.
gnuplot の起動と終了
ではターミナルに gnuplot と入力して起動してみましょう!
istc c-012:~/Gnuplot 0123456s$ gnuplot
G N U P L O T
Version 3.7 patchlevel 2 (+1.2.0rc2 2002/05/05)
last modified Sat Jan 19 15:23:37 GMT 2002
Copyright(C) 1986 - 1993, 1998 - 2002
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual
The gnuplot FAQ is available from
<http://www.ucc.ie/gnuplot/gnuplot-faq.html>
Terminal type set to 'aqua'
gnuplot>
のように, オープニングメッセージとともに gnuplot のプロンプト 「gnuplot>」が現れます. gnuplot を終了するには
gnuplot> exit
または
gnuplot> quit
とします.
なお, 情報基盤センターの設定では, gnuplot を上記のように終了しても グラフのウィンドウは消えないようです. グラフのウィンドウは マウスなどを使って消しましょう.
関数の2次元グラフを描く
まずは sin(x) のグラフを描いてみましょう. プロンプトのところで
gnuplot> plot sin(x)
と入力してみましょう. すると gnuplot のウィンドウが立ち上がり, sin(x) のグラフが現れます.
gnuplot では plot というコマンドを使うことによって 様々な関数のグラフを描くことができます. 表 1 に利用できる関数の 例を示します. もちろん, これらの基本関数を組み合わせた関数のグラフ を描くこともできます.
聞いたことのない関数もあるでしょう. それらは調べてみてください.
| 関数 | 説明 |
| 2 + x | 2+x (もちろん - (マイナス) もあります) |
| 2*x | 2 × x |
| x**2 | x の2 乗 |
| x=2 | x = 2 |
| abs(x) | x の絶対値 |x| |
| acos(x) | arccos(x) |
| arg(x) | 複素数 x の偏角(単位はラジアン) |
| asin(x) | arcsin(x) |
| atan(x) | arctan(x) |
| besj0(x) | x の j0 次ベッセル関数 |
| besj1(x) | x の j1 次ベッセル関数 |
| besy0(x) | x の y0 次ベッセル関数 |
| besy1(x) | x の y1 次ベッセル関数 |
| ceil(x) | x よりも小さくない最小の整数 |
| cos(x) | cos(x) |
| cosh(x) | cosh(x) |
| erf(x) | 実数 x の誤差関数 |
| erfc(x) | 1.0-erf(x) |
| exp(x) | exp |
| gamma(x) | 実数 x のΓ関数 |
| ibeta(p,q,x) | 実数(p,q.x) のibeta 関数 (p, q は数値) |
| inverf(x) | 実数 x の逆誤差関数 |
| igamma(a,x) | 実数(a,x) の igamma 関数 (a は数値) |
| imag(x) | 複素数 x の虚数部 |
| invnorm(x) | 実数 x の逆正規分布関数 |
| int(x) | 実数 x を丸めた整数 |
| lgamma(x) | 実数 x のlgamma 関数 |
| log(x) | 自然対数 loge(x) |
| log10(x) | 10 を底とする対数 log10(x) |
| norm(x) | 実数 x の正規分布(ガウシアン) 関数 |
| sgn(x) | x > 0 ならば 1, x < 0 ならば -1, x = 0 ならば 0 |
| sin(x) | sin (x) |
| sinh(x) | sinh(x) |
| sqrt(x) | x の平方根 |
| tan(x) | tan(x) |
| tanh(x) | tanh(x) |
練習問題
次の関数の図を描いてみましょう. pi は円周率 (=3.141592...) です.
2.0/1.0*sin(1*pi/2)*cos(1*x)
次に, 下の関数の図を描いてみましょう.
2.0/1.0*sin(1*pi/2)*cos(1*x) + 2.0/3.0*sin(3*pi/2)*cos(3*x)
次に, 下の関数の図を描いてみましょう.
2.0/1.0*sin(1*pi/2)*cos(1*x) + 2.0/3.0*sin(3*pi/2)*cos(3*x) + 2.0/5.0*sin(5*pi/2)*cos(5*x)
さらに,
2.0/1.0*sin(1*pi/2)*cos(1*x) + 2.0/3.0*sin(3*pi/2)*cos(3*x) + 2.0/5.0*sin(5*pi/2)*cos(5*x) + 2.0/7.0*sin(7*pi/2)*cos(7*x) + 2.0/9.0*sin(9*pi/2)*cos(9*x) + 2.0/11.0*sin(11*pi/2)*cos(11*x) + 2.0/13.0*sin(13*pi/2)*cos(13*x)
同様にさらに項の数を増やしたとき, 関数はどのような形になるか考えてみましょう.
この関数は, 一般的には,
2.0/1.0*sin(1*pi/2)*cos(1*x) + 2.0/2.0*sin(2*pi/2)*cos(2*x) + 2.0/3.0*sin(3*pi/2)*cos(3*x) + ... + 2.0/n*sin(n*pi/2)*cos(n*x) + ...
と書けます. このように, 周期的な関数を多数の項の和で展開することをフーリエ級数展開と呼びます (惑星学基礎III で扱います).
複数のグラフ
gnuplot では複数の関数やデータを 1 つのグラフに描くことができます. たとえば下のようにすることで, sin(x) と sin(2x) の 2 つの関数を 重ねて描くことができます.
gnuplot> plot sin(x), sin(2*x)
3 つ以上の関数を重ねて書く場合にも, 同様に関数をカンマ (,) で区切って 並べていきます.
複数のグラフ (その 2)
複数の関数やデータを 1 つのグラフに描くとき, 複数のデータの絶対値が 大きく異なるとグラフが見にくくなることがあります. たとえば, sin(x) と 100 cos(x) を一つのグラフに描いてみましょう.
gnuplot> plot sin(x), 100 * cos(x)
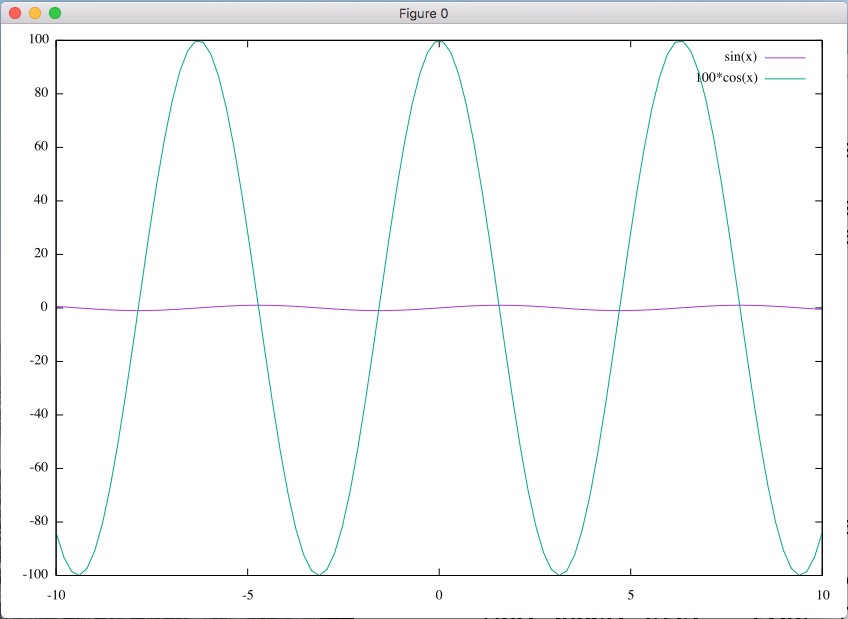
sin(x) と 100 cos(x) の振幅が大きく異なるため, sin(x) の変化が見にくくなっています.
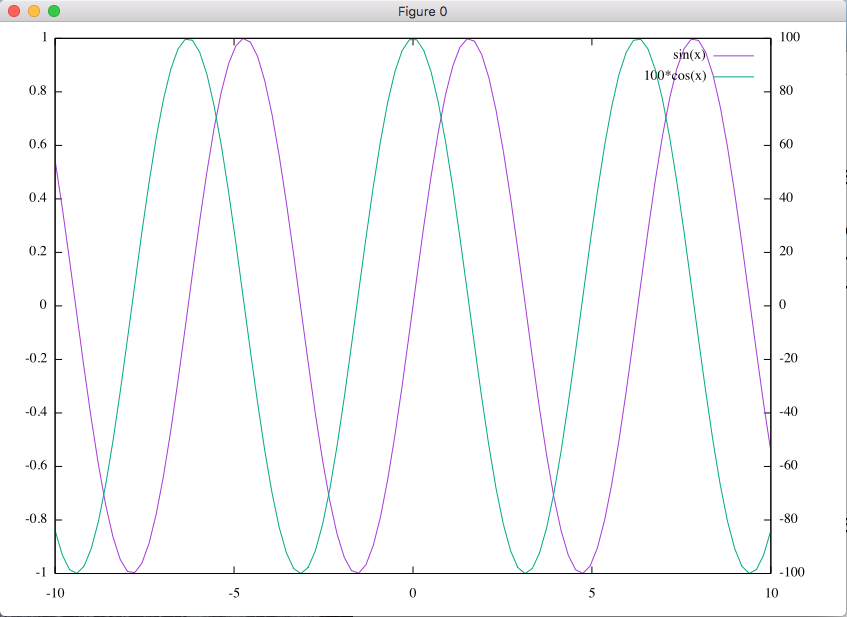
このようなとき, 100 cos(x) の振幅を変えてグラフを描くこともできますが, 下のようにすることでグラフの右側にもう一つの y 軸を設定し, グラフを見やすくすることもできます.
gnuplot> set y2tics <- グラフの右にもう一つ y 軸を設定 gnuplot> set ytics nomirror <- グラフの左の y 軸の目盛りを右側の y 軸に描かないようにする gnuplot> plot sin(x), 100 * cos(x) axes x1y2
axes x1y2 によって, グラフの下の x 軸 (x1 軸; sin(x) の軸と共有) とグラフの右の y 軸 (y2 軸) を使うことを指定しています.
各種設定 (その 1)
点の数の設定
ここまでに描いた関数のグラフは, よく見ると「カクカク」してみえるでしょう. これはグラフを構成する点の数が若干足らないためです.
この点の数を設定するには下のようにします.
gnuplot> set sample 1000 gnuplot> plot sin(x)
なお, 上の例では, 十分にたくさんの数として 1000 点でグラフを描くようにしていますが, 逆に点の数を減らしてみると何が起こるでしょうか. たとえば,
gnuplot> set sample 10 gnuplot> plot sin(x)
とすると, グラフが「カクカク」することはもちろんのこと, sin(x) の振幅も位相も正しく表現されません. これは「サンプリングエラー」のためで, 表現したい変動に対して十分に大きな頻度でデータを得なければならないことを表しています. このことは, 観測装置を使って何かしらを観測するときに当然気を付けなければいけないことです.
軸の範囲の設定
表示する x 軸 y 軸の範囲を設定するには
set xrange [x の最小値: x の最大値]
という命令をつかいます. 例えば, sin(x) の図で x の範囲を 8 から 17, y 軸の範囲を -1.5 から 1.5 に するには, 下のようにします.
gnuplot> set xrange [8:17] gnuplot> set yrange [-1.5:1.5] gnuplot> plot sin(x)
とします. なお,
gnuplot> plot sin(x)
の代わりに
gnuplot> replot
とすると, 最後に実行した plot の命令を再度実行します.
また, 二つの関数のグラフを描くときに関数ごとに範囲を制限することもできます. 例えば,
gnuplot> plot sin(x), sin(2*x)
では sin(x) と sin(2*x) が同じ範囲で描かれますが,
gnuplot> plot sin(x), [-1:1] sin(2*x)
とすると, sin(2*x) は一部の範囲のみ描かれます.
曲線のラベル
sin(x) の図では描かれた線の説明として右上に「sin(x) ―」のような表示が 現れています. この説明表示を「キー (key)」と呼びます. 複数の関数を 1 つのグラフに描く場合は関数の数だけ「キー」が表示されます. グラフを描く場合は, 以下のようなコマンドを使って, それぞれの線の意味が わかるように「キー」の内容を適切なものにしておくことが大切です.
gnuplot> plot sin(x) title "sleepines"
システムによっては, キーに日本語を書き込むと文字化けすることが 珍しくありません. 英語またはローマ字で書きましょう.
複数の関数を書くときは下のように指定します.
gnuplot> plot sin(x) title "sleepiness",sin(2*x) title "happiness"
また、「キー」がグラフと重なった場合などは、
set key at x, y
という命令で好みの位置にずらすことができます. ここで x, y はグラフ上の座標です. 例えば
gnuplot> set key at 9.5,1.2 gnuplot> replot
とします.
軸目盛の設定
軸の目盛のきざみ方は次のような命令で変えることができます.
set xtics x の最小値x のきざみx の最大値
たとえば, x 軸のきざみは 1, y 軸のきざみは 0.5 (目盛をつける x 軸の 範囲は 8 から 17, y 軸の範囲は -1.5 から 1.5) にしたい場合,
gnuplot> set xtics 8,1,17 gnuplot> set ytics -1.5,0.5,1.5 gnuplot> replot
のようにします.
なお, 今後のために, メモリ刻みを元に戻しておきましょう.
gnuplot> set xtics auto gnuplot> set ytics auto
軸目盛の数値を斜めに書く
なお, ここで示す例でグラフに書かれる数値は見にくくありませんが, グラフの目盛りに書かれる数値が「長い」場合 (例えば 1.234567890 のように 文字が多い場合), 数値が重なってしまうため見にくくなることがあります. そのようなときには, 目盛りの数値を斜めに書くことで重ならないように工夫 することができます.
例えば下のようにしてみましょう.
gnuplot> set xtics rotate by -30 gnuplot> replot
x 軸の目盛りの数値が -30°傾いて書かれます.
軸のラベル
グラフを描くときは, 軸の意味が分かるように軸に適切なラベルを 付けなくてはいけません. 軸のラベルは下のように指定します.
gnuplot> set xlabel "time [hour]" gnuplot> set ylabel "relative value" gnuplot> replot
で指定します.
なお, 軸のラベルでは "_" や "^" を使うことで上付き文字や下付き文字を書くこともできます. 例えば下の例では, x に下付き文字 1 を付け, 上付き文字で 3 を書いています. つまり, x1 の二乗ですね.
gnuplot> set ylabel "x_{1}^{2}"
下付き文字や上付き文字は数字である必要はありませんし, より複雑にすることもできます. 例えば,
gnuplot> set ylabel "x_{start}^{x^{test}}"
はどうなるでしょうか? (set xlabel, set ylabel を指定するだけではグラフは変化しません. plot や replot とすることでグラフが描き変わります.)
また, 下のようにすることでギリシア文字を使うこともできます.
gnuplot> set xlabel "{/Symbol abcdefg p}"
変数や関数の定義
sin(x) などは簡単な関数なので, キーボードを打つのも簡単ですが, 複雑な関数のグラフを描きたい時などは, 変数や関数を定義して使えると便利なことがあります. 例えば, 下では, プランク関数のグラフを描いてみましょう. プランク関数は, ある温度 T (K) を持った物体が出している電磁波エネルギーの スペクトルを表しています.
まず, いくつかの定数を定義します.
gnuplot> bol = 1.38e-23 gnuplot> sol = 3.00e8 gnuplot> pla = 6.63e-34 gnuplot> temp = 6000
上で定義した定数はそれぞれ, bol : ボルツマン定数, sol : 光速度, pla : プランク定数, temp : 温度です. そして, プランク関数を定義します.
gnuplot> B(x) = 2*pla*sol**2 / x**5 / ( exp( pla*sol/(x*bol*temp) ) - 1 )
ここで, x は波長を表しています. なお, 上で示した値はすべて MKS 単位系での数値です.
では, この関数 B(x) をプロットしてみましょう.
gnuplot> plot B(x)
ただし, このグラフでは良くわかりませんので, 軸を変えてみましょう. ここでは, 横軸の範囲を 1e-7 から 1e-4 とし, 縦軸の範囲を 1e5 から 1e14 として, 縦軸, 横軸ともに対数軸にしてみましょう. 1e-7, 1e-4 はそれぞれ 10 の -7 乗と 10 の -4 乗を表します. (図の範囲を指定する方法は上で説明しました.)
縦軸を対数軸にするには, 下のように入力します.
gnuplot> set logscale y
x 軸も y 軸も対数軸にするときには下のように入力します.
gnuplot> set logscale
すると, 下のようなグラフが描けるはずです.
6000 K のプランク関数は, おおよそ太陽のスペクトルに対応しています. 太陽は, 紫外線, 可視光線, 赤外線といった様々な波長の光を射出していますが, 最も多くの射出しているのは可視光線です. そのことは, 関数のピークがおよそ 5e-7 (m) = 0.5 μm のところにあることから もわかります. 0.5 μm は, およそ緑色をした可視光線です.
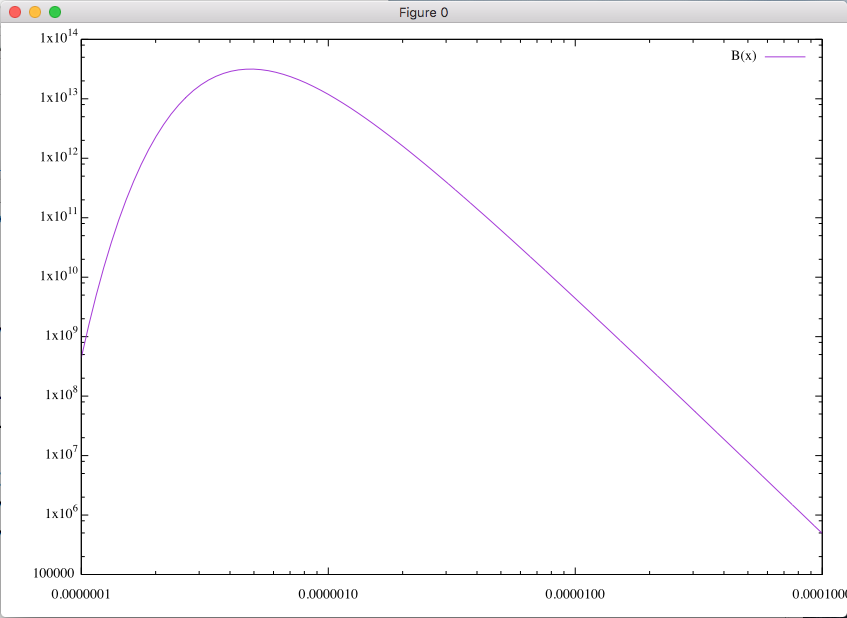
また, 対数軸をやめるときには下のように入力します.
gnuplot> unset logscale y
関数の 3 次元グラフを描く
GNUPLOT では 3 次元 (x,y,z) のグラフも書くことができます. しかしここでは簡単な説明のみとします.
3 次元のグラフのための命令文は splot です. 例として
gnuplot> splot sin(x)*y
と入力してみましょう. 3 次元の波打ったグラフがあらわれるはずです.
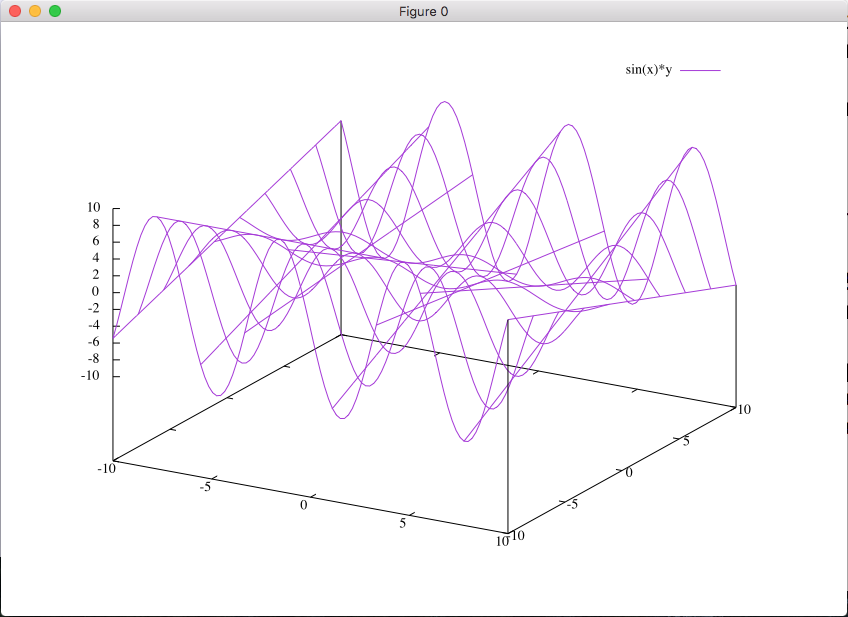
メッシュの数を変える
3 次元関数のグラフでは曲面は格子状の線分(メッシュ)で表示されます. メッシュの本数は
set isosample y 軸方向に描かれる本数 x 軸方向に描かれる本数
と指定します. 特に自分で設定を変えなければ (これを「デフォルト」と呼びます), メッシュの本数はそれぞれ 10 本です. 例えば,
gnuplot> set isosample 50,50 gnuplot> replot
としてみましょう. よりきめの細かいグラフになります.
曲面の重なり表示させない
先に描いた 3 次元のグラフでは, 曲面が視線方向に重なっている場所でも すべての線が表示されているのでちょっと見にくくなっています. 曲面の重なりを表示させないためには
gnuplot> set hidden3d gnuplot> replot
とします. 逆に, 重なった部分も表示する状態にもどすには
gnuplot> unset hidden3d gnuplot> replot
とします.
視点の変化
3 次元のグラフは, 視点の位置によって見えやすさが大きく異なるものです.
コマンドで視点を変化させるには下のように入力しましょう.
gnuplot> set view 30, 60
この例では, x 軸周りに 30 度回転させ, z 軸周りに 60 度回転させた視点になります.
等値線の表示
3 次元の曲面の表示がわかりやすい時もありますが, 等値線の方が分かりやすいこともあるでしょう. 等値線を表示するには下のようにします.
gnuplot> set contour gnuplot> replot
こうすることで, 曲面の下に等値線分布が描かれるでしょう. さらに, 等値線の数を増やしたいならば下のようにしましょう.
gnuplot> set cntrparam levels 10 gnuplot> replot
この例では 10 本の等値線を引くように設定しています.
しかし, これでは等値線が曲面に隠されてしまうかもしれません. そんなときには下のようにして曲面を消しましょう.
gnuplot> unset surface gnuplot> replot
曲面が消えて等値線が見やすくなるでしょう. さらに
gnuplot> set view 0,0 gnuplot> replot
とすれば, 等値線がより見やすくなるかもしれもしれません.
ファイルの中のデータをプロットする (その 1)
ここまでは関数のグラフを書かせる方法を練習しましたが, 実用では 関数よりも実験や数値計算の結果をグラフにしたい場合のほうが多いでしょう. ここでは, 表形式でまとめられた実験(観測)結果をもとにグラフを描いてみましょう.
まず, データを用意するために下のファイルをダウンロードしましょう.
- 火星大気温度の高度分布
- 注意:
- ブラウザで上のデータファイルのリンクをクリックすると, ファイルが開かれます. この時に, 日本語が文字化けしているかもしれません. このような時には, モニタの上部にある Safari のバーの「表示」->「テキストエンコーディング」->「Unicode (UTF-8)」を選ぶと良いでしょう.
- 注意:
ダウンロードするためには, ターミナルで下のようにコマンドを実行します.
istc c-012:~012345s$ curl http://itpass.scitec.kobe-u.ac.jp/~itbase/exp/fy2021/gnuplot_data/renshuu.txt -O
注意: 最後の "-O" は「ハイフン」「(大文字)オー」です.
コピーしたデータの内容を less で見てみましょう.
istc c-012:~012345s$ less renshuu.txt
ファイルの上部には, "#" で始まる行にデータの説明が書かれています. "#" で始まる行は, gnuplot ではグラフを描く際には無視されます.
renshuu.txt のデータを使ってグラフを描くには
gnuplot> plot "renshuu.txt" with linespoints
とします.

このグラフは, 火星探査機 Mars Pathfinder が観測した火星大気の温度の 高度分布です. 横軸が高度 (km) で, 縦軸が温度 (K) になっています.
しかし, 私たちの感覚として, 高度は縦に伸びる軸ですから, 高度を縦軸にした方が直感的でしょう. そのような時には, 使うデータの順番を下のように指定することができます.
gnuplot> plot "renshuu.txt" using 2:1 with linespoints
using 2:1 は, x 軸は 2 カラム目, y 軸は 1 カラム目の値を使うことを意味します.
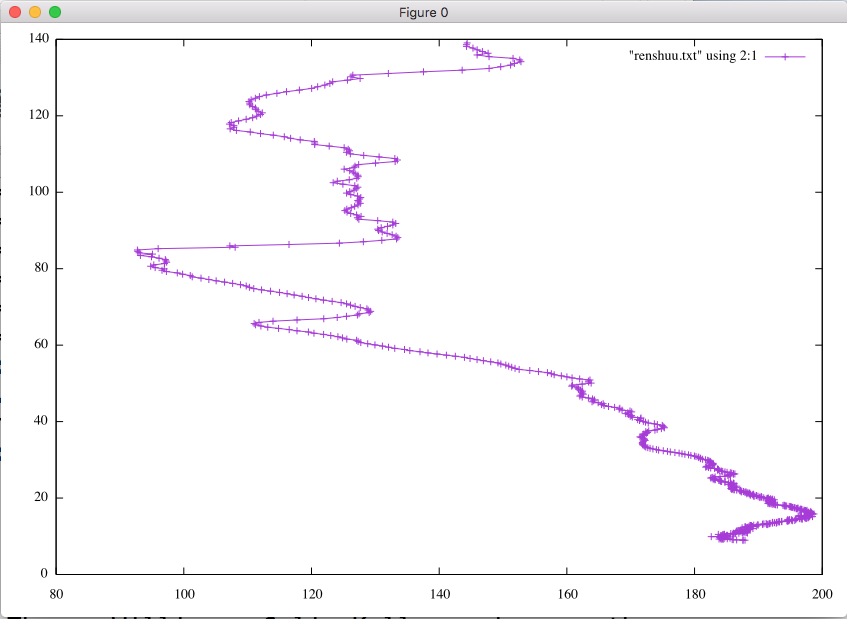
この図では横軸が温度 (K) で縦軸が高度 (km) です. これから, 高さが高くなると火星の大気温度がどのように変動しているか 読み取ることができるでしょう.
また, renshuu.txt に保存されている温度の単位は絶対温度, K, ですが, 単位を変更したいこともあるでしょう. 例えば, 摂氏, °, を単位としてグラフを描きたい時には, 横軸の値から 273.15 を 引けば良いので, 下のように指定します.
gnuplot> plot "renshuu.txt" using ($2-273.15):1 with linespoints
このように, using に "$カラムの番号" と書くことで演算を行うこともできます.
さらに, その演算には, 複数の "$カラムの番号" を使って 演算することもできます. 例えば,
gnuplot> gasc = 8.31/44e-3 gnuplot> plot "renshuu.txt" using ($5/(gasc*$2)):1 with linespoints
とすると, 横軸が密度 (kg m-3), 縦軸が高度 (m) のグラフとなります. ここで, gasc = 8.31/44e-3 は気体定数です (8.31 (J K-1 kg-1) は普遍気体定数で, 44e-3 は二酸化炭素の分子量 (kg mol-1)). また, using に指定されている $5 は圧力で, $2 が温度ですから, 理想気体の状態方程式により, $5/(gasc*$2) は密度を表します.
各種設定 (その 2)
線と点の種類
先に書いた図では「十字」の印で表されたデータ点 (point) が, 実線 (line) でつながれていますが, この point や line には いくつか種類があって, 自由に変えることができます. 一つの図に複数の実験データを書きこむ場合には, 実験データ ごとに line や point を変えます. 例えば,
gnuplot> plot "renshuu.txt" with linespoints linetype 0 pointtype 5
としてみましょう. line と point が変わったはずです. 上記では line の種類を 0 番に指定して, point の種類を 5 番に指定して います. 番号の指定をいろいろ変えて, どのような表示になるか確かめて みましょう. linespoints は lp, linetype は lt, pointtype は pt と略すことができます. 例えば, 下のように打つこともできます.
gnuplot> plot "renshuu.txt" with lp lt 0 pt 5
| スタイル | 説明 |
| lines | 線で表示 |
| points | 点で表示 |
| linespoints | 点で表示したデータを線で結ぶ |
| impulses | インパルス表示 |
| dots | ドット(小さい点) で表示 |
| steps | ステップ表示 |
| errorbars | 誤差つきの表示 |
| boxes | 棒グラフ |
| boxerrorbars | 誤差つき棒グラフ |
グラフのスタイル
グラフを line だけ, または point だけで書きたいときは
gnuplot> plot "renshuu.txt" with lines gnuplot> plot "renshuu.txt" with points
または
gnuplot> set style data lines gnuplot> plot "renshuu.txt"
のようにします. グラフのスタイルは ``lines'',''points'', ``linespoints'' のほかにも いろいろあります.
次に誤差 (エラーバー) つきのグラフを書いてみましょう. 誤差つきのグラフを書くときは, 当然, もとのデータ表に誤差の情報を 書いておく必要があります. renshuu.txt の中には, 3, 4 カラム目に温度の下限値と上限値が含まれています.
これを使って,
gnuplot> plot "renshuu.txt" using 1:2:3:4 with errorbars
とすれば, 誤差つきのグラフが描けます.
また, 上に述べたように, 高度は縦軸にしたいものです. その上で誤差の 付いたグラフにするには下のようにします.
gnuplot> plot "renshuu.txt" using 2:1:3:4 with xerrorbars
このときには, using によって, 横軸の値:縦軸の値:横軸方向の最小値:横軸方向の最大値 を指定しています.
複数の線を一つのグラフに描く
また, renshuu.txt の中の温度の下限値と上限値を, それぞれ 1 本ずつの 線として, 複数の線を一つのグラフに重ね描きしてみましょう.
plot "renshuu.txt" using 2:1 with linespoints, "renshuu.txt" using 3:1 with linespoints, "renshuu.txt" using 4:1 with linespoints
これにより, 3 本の線が描かれます.
また, 複数のデータを一つのグラフに描く方法はもう一つあります. それは, 複数のファイルにそれぞれデータを格納しておく方法です. この時は, 関数を描く方法で説明したのと同様にして, plot コマンドのあとにカンマ(,) で区切って
plot "file1", "file2"
とします.
対数軸
次に, renshuu.txt の 5 カラム目にある圧力の高度分布を描いてみましょう.
gnuplot> plot "renshuu.txt" using 5:1 with lines
圧力は, 高度とともに急激に (指数関数的に) 変化していることがわかります. しかし, 圧力の変化が急激であるため, 高高度の圧力は読み取りにくくなって います. そこで, 下のようにして横軸を対数軸にしてみましょう.
gnuplot> set logscale x gnuplot> replot
対数軸では, 圧力が高度に対して直線に近い変化をしていることがわかります.
なお, 線形の軸に戻したい時には下のようにします.
gnuplot> unset logscale x
また, y 軸を対数軸にするには,
gnuplot> set logscale y
とし, x 軸, y 軸の両方を対数軸にするには,
gnuplot> set logscale
とします.
ファイルの中のデータをプロットする (その 2)
次に時間の軸を持ったデータを使ってグラフを描いてみましょう. まず, データを用意するために下のファイルをダウンロードしましょう.
そしてこれらのファイルの内容を見てみましょう.
例えば気圧のファイル (Kobe-kisho_Ps.txt) であれば, 下のような内容が含まれているでしょう.
# 神戸地方気象台における現地気圧 # (http://www.data.jma.go.jp/gmd/risk/obsdl/index.php) # <1st column>: 日時 / Date and Time (年-月-日-時) # <2nd column>: 現地気圧 / Pressure (hPa) 2018-12-01-01 1019.8 2018-12-01-02 1019.7 2018-12-01-03 1019.6 2018-12-01-04 1019.4 2018-12-01-05 1019.5 2018-12-01-06 1019.8 2018-12-01-07 1020.2 2018-12-01-08 1020.7 2018-12-01-09 1021.1 2018-12-01-10 1021.4 2018-12-01-11 1021.5 2018-12-01-12 1020.6
gnuplot を使ってこのデータのグラフを描く際に, 下のように入力するだけでは現地気圧の時間変化のグラフを描くことはできません.
gnuplot> plot "Kobe-kisho_Ps.txt" w l
それは, gnuplot が日時の指定を解釈できないためです. gnuplot に横軸が時間軸であり, データファイルに上のような書式で日時が保存されていることを設定するためには下のようにします.
gnuplot> set xdata time gnuplot> set timefmt "%Y-%m-%d-%H"
ここで, %Y, %m, %d, %H はそれぞれ年, 月, 日, 時間 (24 時間表示) を表し, 上の set timefmt はそれら 4 つの数字がハイフン ("-") で繋がった文字列 によって時刻が表記されていることを設定しています.
その上で
gnuplot> plot "Kobe-kisho_Ps.txt" u 1:2 w l
とすることで時間変化のグラフを描くことができるでしょう.
同じように降水量, 気温のグラフも描いてみましょう.
また, グラフの横軸 (時間軸) の範囲を変更するには下のようにしましょう.
gnuplot> set xrange ["2019-06-01-01":"2019-06-30-24"] gnuplot> plot "Kobe-kisho_Ps.txt" u 1:2 w l
気圧のグラフを見ると, 大きく気圧が下がっている日を見つけることができるでしょう. この日の天気図を検索するなどして, この日に何が起こっていたのか確認してみましょう. また, その時の降水量と気温はどのように変化しているでしょうか.
ファイルの中のデータをプロットする (その 3)
まず, データを用意するために下のファイルをダウンロードしましょう.
ファイルの内容を確認すると, 経度, 緯度, 標高の数値が並んでいることがわかります. このデータを 3 次元で描画するには, 関数の描画と同様に splot を使います.
gnuplot> splot "topography_Earth.txt" w l
下にある金星と火星の地形の分布も確認してみましょう.
なお, このようにファイルに保存されたデータから 3 次元のグラフを描くためには, データファイルの形式に注意する必要があります. 上の地球の地形のファイルでは,
0.0000000000000000 -88.927735352295912 2688.8912848158129
1.4062500000000000 -88.927735352295912 2691.3416204217538
2.8125000000000000 -88.927735352295912 2694.8297394429469
...
357.18750000000000 -88.927735352295912 2681.6849730458221
358.59375000000000 -88.927735352295912 2685.5880255534098
<- 空行
0.0000000000000000 -87.538705213027171 2586.6998299319730
1.4062500000000000 -87.538705213027171 2595.0596638655461
2.8125000000000000 -87.538705213027171 2607.3696145124718
...
357.18750000000000 -87.538705213027171 2565.4467120181407
358.59375000000000 -87.538705213027171 2576.8119610048743
<- 空行
0.0000000000000000 -86.141472101527896 2596.2045324153760
1.4062500000000000 -86.141472101527896 2603.6090715804394
...
のように, 緯度が変わるところに空行を入れる必要があります. 自分でデータを用意するときには注意しましょう.
グラフの保存
これまでは, グラフを画面に描いていましたが, グラフをファイルに保存する ことでレポートや卒業論文に貼ることができるようになります. グラフを保存する際には様々な形式を利用することができますが, ここでは, pdf 形式と png 形式で保存することにします.
ここでは, 上で行った,
gnuplot> plot "renshuu.txt" using 5:1 with lines
で出力されるグラフをファイルに保存してみましょう. pdf ファイルで保存するためには, 下のようにコマンドを入力します.
gnuplot> set terminal pdf gnuplot> set output "renshuu.pdf" gnuplot> plot "renshuu.txt" using 5:1 with lines gnuplot> set terminal x11
なお, 上の 3 行目 plot "renshuu.txt" ... は, 入力しても画面にグラフは表示されませんので注意してください.
一つずつコマンドの役割を確認してみましょう.
gnuplot> set terminal pdf
は, 出力の形式を指定しています. 一般に,
gnuplot> set terminal <形式>
とします. なお, 上の set terminal pdf を実施する前は, 画面に出力するための 形式が指定されていたことになります (具体的には形式として x11 が 指定されていたことになります).
次に,
gnuplot> set output "renshuu.pdf"
は, ファイル名を指定しています.
次の
gnuplot> plot "renshuu.txt" using 5:1 with lines
で, 「ファイルにグラフを描いています」. この時は, set terminal と set output で, 出力形式と出力ファイル名が していされているので, グラフは画面に描かれません.
そして最後の
gnuplot> set terminal x11
は, 出力先をファイルから画面に戻すコマンドです. これを打たないと, gnuplot はファイルへの保存が終了せず, 画像ファイルは 空のままになっています. set terminal x11 をすることによって, 画像ファイルへの保存が完了します.
もし png 形式でグラフを保存したい時には,
gnuplot> set terminal pdf gnuplot> set output "renshuu.pdf"
を
gnuplot> set terminal png gnuplot> set output "renshuu.png"
とします.
また, 作成した pdf ファイルの内容を確認するには, open コマンドを使います. (基盤センターや macOS では.)
istc c-012:~ 0123456s$ open renshuu.pdf
また, 仮想環境では evince コマンドを使います.
$ evince renshuu.pdf
open や evince は gnuplot のコマンドではないことに注意しましょう.
スクリプトファイルを使う
ここまでに行ったようなコマンドのセットをファイルに書いておくと, load コマンドで間単に図を描くことができます. このテキストファイルをスクリプトファイルと呼びます.
試しに emacs で sleep.txt というファイルを作ってみましょう. まずターミナルから emacs を立ち上げます。
istc c-012:~012345s$ emacs sleep.txt &
emacs に以下を入力します.
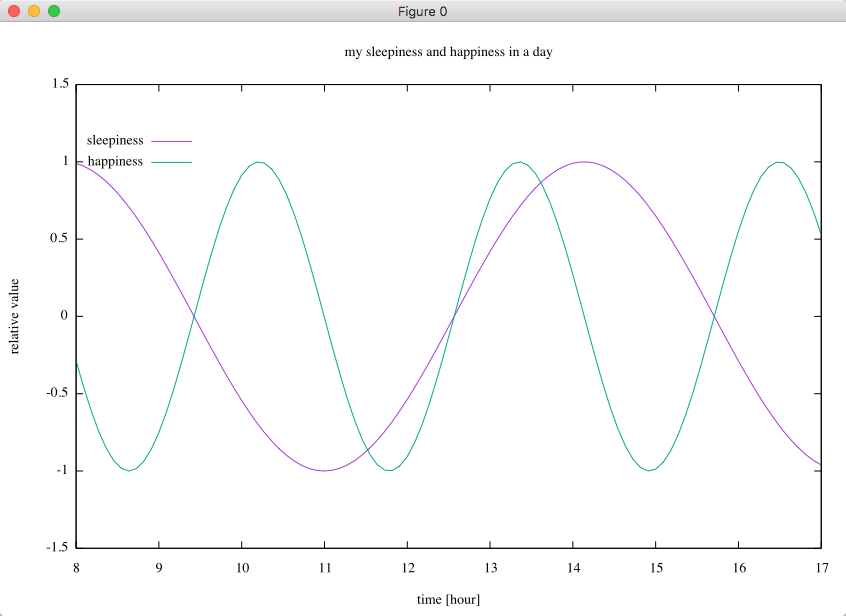
set xrange [8:17] set yrange [-1.5:1.5] set xtics 8,1,17 set ytics -1.5,0.5,1.5 set xlabel "time [hour]" set ylabel "relative value" set title "my sleepiness and happiness in a day" set key at 9.5,1.2 plot sin(x) title "sleepiness", sin(2*x) title "happiness"
書き終わったらファイルを保存します. gnuplot を起動して
gnuplot> load "sleep.txt"
と入力してみましょう. 図が描けるはずです. このようなスクリプトファイルを 1 つ用意しておくと, 一部のパラメータを書き換えるだけで簡単に他のグラフも描けるので便利です.
マニュアル
gnuplot には様々なコマンドが用意されています. それらについて調べたいときには "?" コマンドを使うと良いでしょう.
例えば, plot の使い方を調べたい時には,
gnuplot> ?plot
とすると説明が表示されます. 説明から抜けたい時には "q" を押しましょう.
また, google などで検索してもたくさんの情報を見つけることができるでしょう.
Keyword(s):
References:[[itbase2021]惑星学実験実習の基礎II]