[itbase2024]Fortran モンテカルロ法による円周率の計算
0 から 1 の間の多数の乱数のうち, 値二つを組みにして, 0 <= x <= 1 かつ 0 <= y <= 1 の正方形の領域内に 多数の点の座標を生成します (下の図参照). 多数の乱数を使うことで多数の点を生成すると, 点の座標は下のようになるでしょう.
( x , y ) (乱数1,乱数2) (乱数3,乱数4) (乱数5,乱数6) (乱数7,乱数8) ...
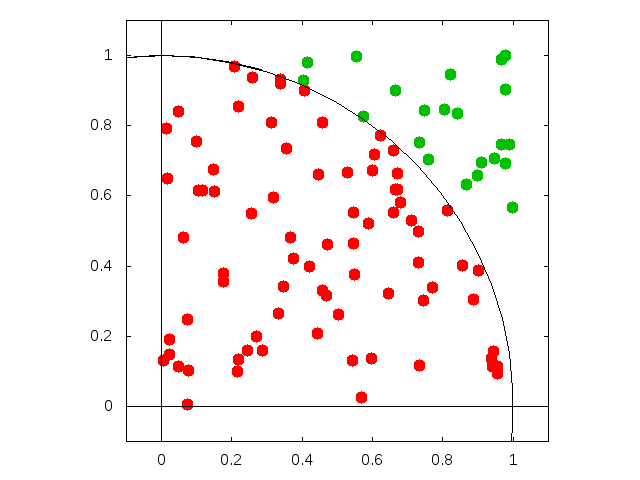
これらの点の中には, 原点を中心とする半径 1 の円内に位置する点 (図中の赤の点) と それから外れる点 (図中の緑の点) があるでしょう.
一方, 原点を中心とする半径 1 の円の面積はπで, そのうちの 0 <= x <= 1 かつ 0 <= y <= 1 の領域内にある面積は π/4 です. したがって, 生成された多数の点のうちの, 半径 1 の円内に収まる 点 (図中の赤の点) と, すべての点 (図中の赤の点と緑の点) の数の 割合は π/4 になることが期待されます. このように点の数の比から求めた値に 4 を掛けることで, 円周率の近似値を求めることができるはずです.
また, 生成する点の数を変えることで, 求めた円周率の値が真の値に どの程度近づくか確認しなさい.
Keyword(s):
References:[[itbase2024]Fortran 入出力・条件分岐・繰り返し 練習問題]