実習で利用したアプリケーションは、初期条件を変えるたびに再度コンパイルする必要があった。また、ソルバは2次のルンゲ=クッタ法のみであった。そこで、今回のレポートでは3体問題の軌道をシミュレーションするGUIアプリケーションを作成した。このソフトでは、アプリケーションを操作する中で初期条件(factorやxp3の値など)を変化させ、再度コンパイルすることなくシミュレーションできる。また、ソルバとしてはEuler法、2次のRunge Kutta法、4次のRunge Kutta法の3つを用意した。
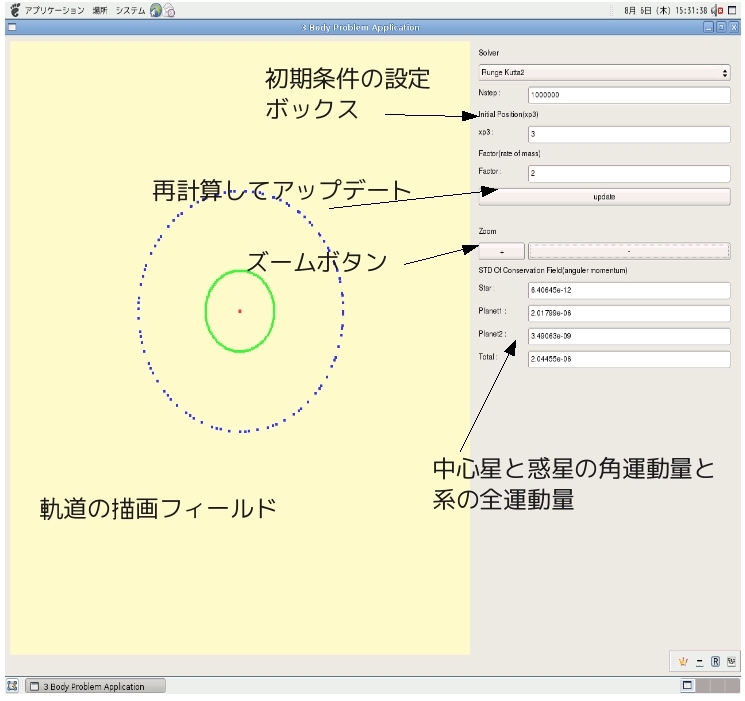
下図は、作成したアプリケーションのスクリーンショットである。右側のパネルの上段で初期条件(ソルバ、ステップ数、xp3、factor)を決める。そして、updateボタンを押せば計算結果が左のパネルに表示される。同時に、角運動量変動具合が標準偏差となって右側パネル下段のテキストボックスに表示される。なお、ズームボタンの+やーを押すことで拡大や縮小表示をすることができる。