授業中に初期条件として考えた条件は
次に、3つのパターンで見られる特徴的な軌道を以下に示す。
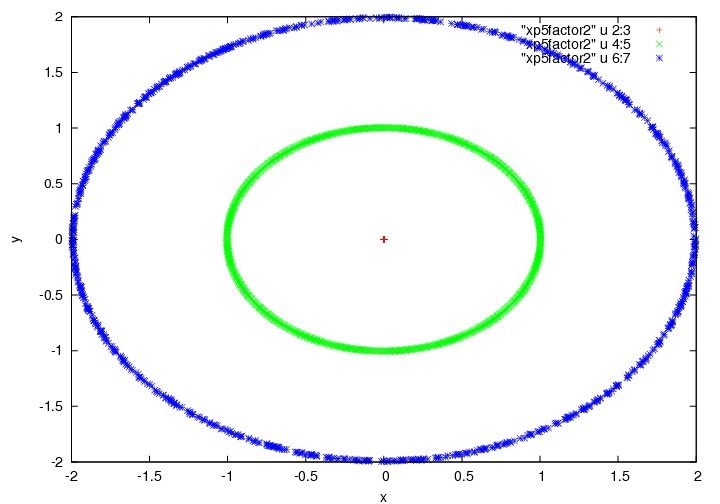
中心星の周りを2つの惑星が楕円軌道している。このパターンでも、外側の惑星の軌道にやや幅があるパターンも存在した。
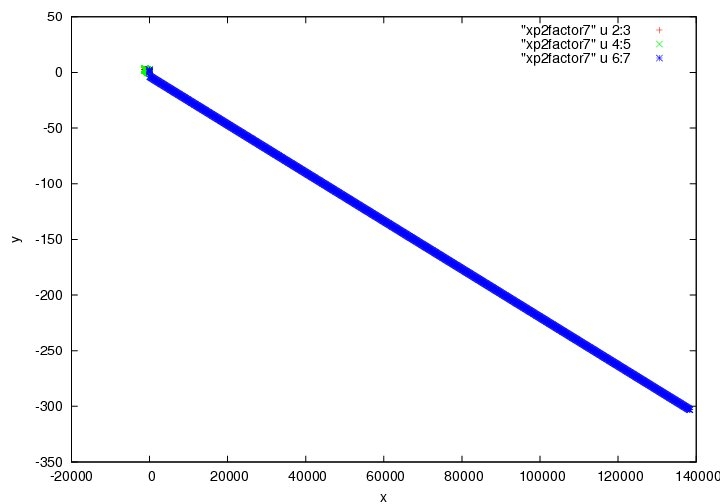
外側の惑星が中心星の引力にとらわれず遠方に遠のいている。また、中心星の周りを拡大すると螺旋模様を見て取ることができた。
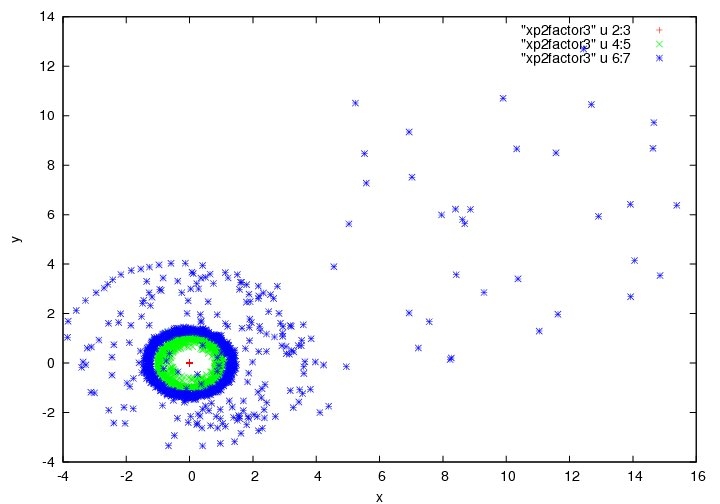
大方、外側の惑星も中心星のまわりを楕円軌道しているようにも見えるが、一部大きく楕円軌道を外れる場合があるパターンを示している。
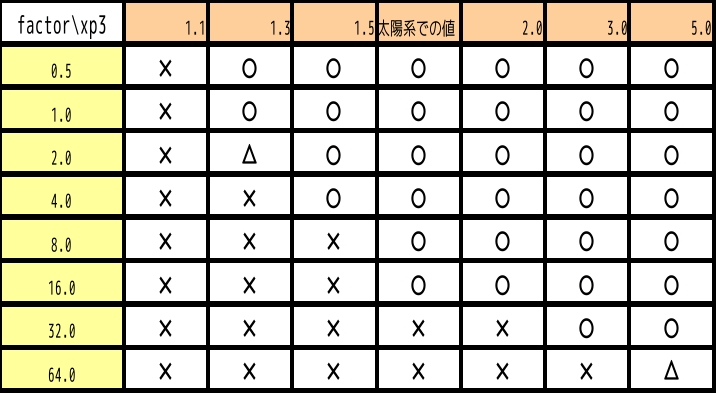
xp3が大きいほど、またfactorが小さいほど3体問題における惑星の軌道は、楕円軌道となり安定となる。これは、xp3が大きいことは外側の惑星が内側の惑星や中心星に与える影響が少なくなることを意味することと一致する。また逆に言えば、相対的に内側の惑星や中心星が外側の軌道を束縛しないとも言える。一方でfactorが小さいことは、中心星に対して外側の惑星の質量が小さいことを意味し、これもまた外側の惑星が内側の惑星や中心星に与える影響が少なくなることを意味する。
ところで軌道が不安定であるかどうかについてだが、その原因が初期条件からくるものなのか、数値計算の誤差からくるものなのかもう少し考察が必要なような気がする。3体問題における数値計算の精度について 自作のソフトウエアを通して「エクストラ課題:惑星運動でみる数値計算の精度」にてもう少し考えてみたいと思う。