おまけ1のようにエネルギー保存が成り立たなくなってしまった原因を考える.
全エネルギーは運動エネルギーとポテンシャルエネルギーの和であり,ポテンシャルエネルギーの項にのみ,万有引力定数がかかっている. しかし,今回のプログラムでは簡単化のために万有引力定数を1としている.そのため,運動エネルギーとポテンシャルエネルギーのスケールの違いが生じてしまい,エネルギーが保存しなかったと考えられる.
そこで,万有引力定数を考慮したプログラムをつくり,おまけ1で調べたパラメータについて,もう一度エネルギーの変化の様子を調べた.
万有引力定数Gを考慮する方法として,プログラムのすべてのパラメータの単位をそろえる方法がある.しかし,今回は精度は落ちるが,プログラム内でGを計算し,そのGを用いてエネルギーを計算する方法を用いた.
時刻1での系の運動エネルギーを K1 ,ポテンシャルエネルギーを U1 とする.このときポテンシャルエネルギーは u1 を用いてU1=Gu1と表せる.同様に時刻2での系の運動エネルギーを K2,ポテンシャルエネルギーを U2 = G u2 とする.系のエネルギーが保存するとき,運動エネルギーとポテンシャルエネルギーの和は一定なので K1 + G u1 = K2 + G u2 となる.この式を整理すると G = (K1 - K2) / (u2 - u1)となり,Gが求まる.この方法でGを計算し,エネルギー保存の様子を調べた.
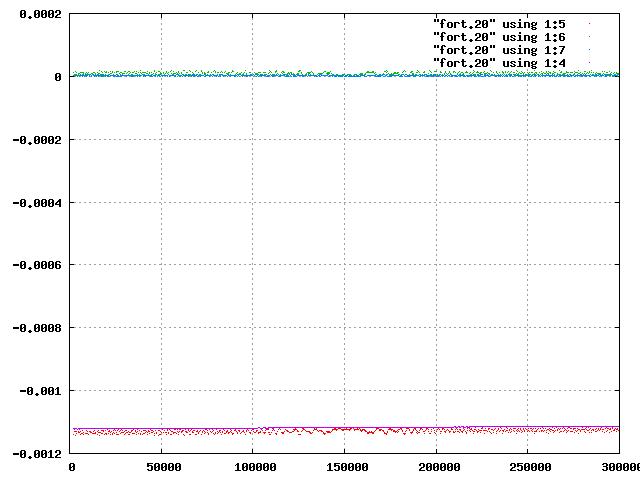
おまけ1と同様にfactor=2,xp(3)=1.5の場合と,factor=5,xp(3)=1.55の場合を調べ,比較した.なお図では横軸にtime,縦軸にエネルギーをとっており,赤が中心星,緑が内側の惑星,青が外側の惑星,紫が系全体の力学的エネルギーを表している.
| 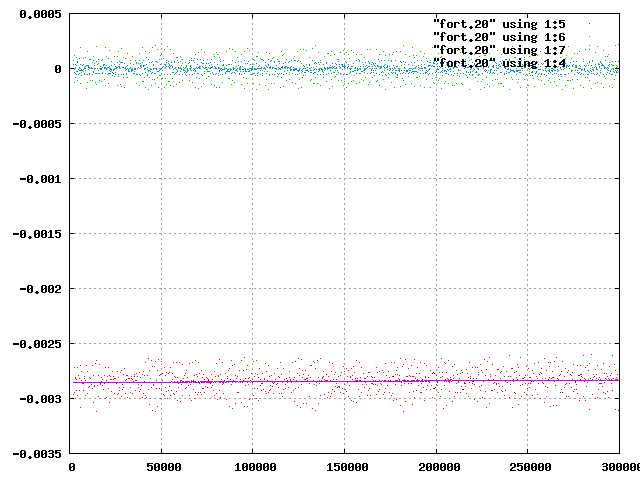 |
| 図8 factor=2,xp(3)=1.5の全エネルギー | 図9 factor=5,xp(3)=1.55の全エネルギー |
おまけ1と同様に軌道にばらつきのあるfactor=5,xp(3)=1.55の方が,個々の天体の力学的エネルギーがばらついていることがわかる.ただし,紫の系全体のエネルギーに注目すると,どちらも一定で保存されている.これより,系の個々の天体が互いにエネルギーを交換しあって,系全体のエネルギーを一定に保っているといえる.
惑星が飛んでしまうfactor=6,xp(3)=1.4とfactor=6,xp(3)=1.55の場合のエネルギーの様子を調べた.
| 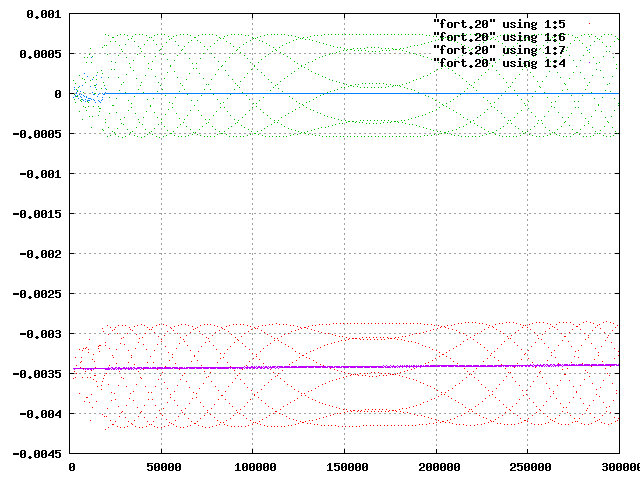 |
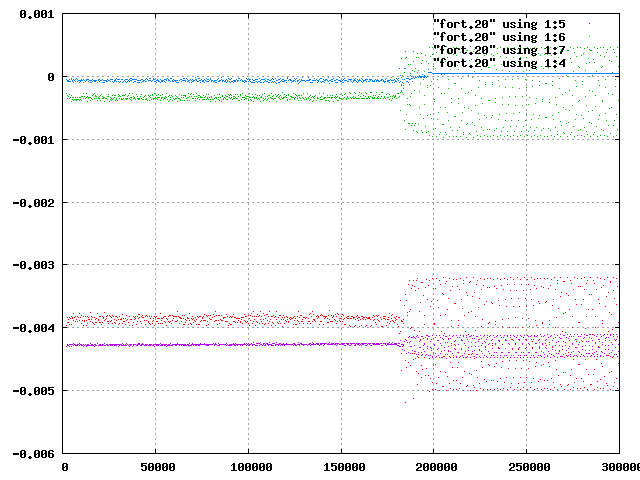
| 図10 factor=6,xp(3)=1.4の全エネルギー | 図11 factor=6,xp(3)=1.55の全エネルギー |
おまけ1の図5と図11を比べると,外側の惑星が飛びだす時刻と,惑星エネルギーの変動が大きくなる時刻が一致していることがわかる.また,これらの図からGを調節しても,エネルギー保存は正確には成り立っていないことがわかる.これは,Gを二つの時刻でのエネルギーから算出している値なので,その他の時刻では計算の誤差が生じているためと考えられる.また,プロットとプロットの間に急激な運動の変化があった場合にも,計算の誤差が生じると考えられる.
一方,図10に注目すると,エネルギーの誤差が大きくなる時刻の前後で,外側の惑星の力学的エネルギーが増加していることがわかる.このことから,惑星が楕円軌道でなくなるとき,その惑星のエネルギーの状態も変化していることがわかる.
△のfactor=3,xp(3)=1.4,maxtime=700000とした場合のエネルギーの様子を調べた.
| 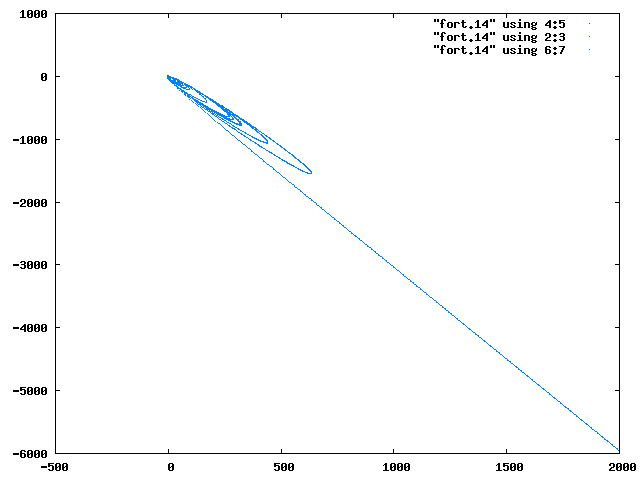 |
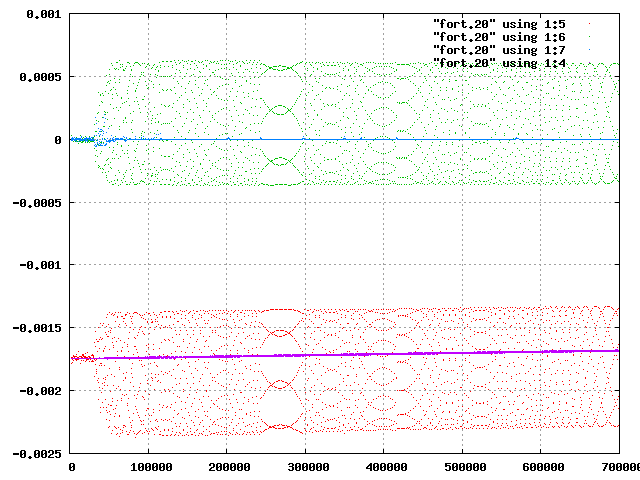
| 図12 factor=3,xp(3)=1.4の全エネルギー | 図13 maxtime=700000,factor=3,xp(3)=1.4の軌道 |
図12より外側の惑星が不安定な楕円軌道を描いているとき,中心星と内側の惑星の力学的エネルギーが変動して,系全体のエネルギーが保存されていることがわかる.また,課題2ではfactor=3,xp(3)=1.4は軌道が閉じていて△としたが,図13より外側の惑星は時間がたつと,他の二つの天体の重力圏から脱出し,timeが700000では×であるということがわかった.したがって,課題2で調べた他のパラメータの計算結果も時間によってかわり,より長い時間で計算すれば表の境界がはっきりする可能性がある.
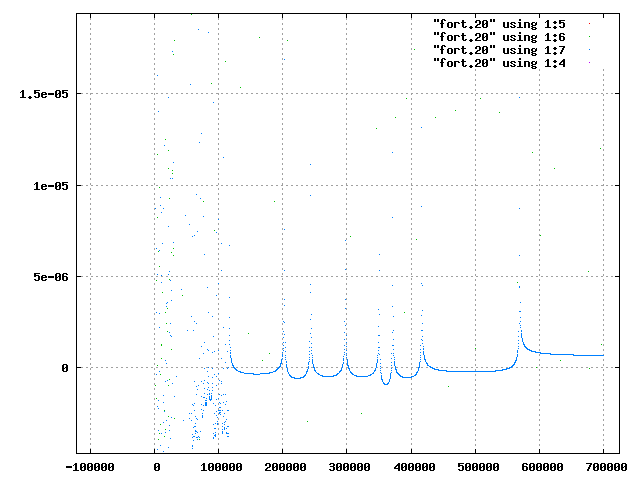
惑星が他の二つの天体の重力圏から脱出するとき,惑星のエネルギーはどのように変化するかを考えるために,図12の外側の惑星のエネルギーについての拡大図を図14に,エネルギーと運動の様子を考えるために図15にfactor=3,xp(3)=1.4の外側の惑星のx方向の時間変化を示す.
| 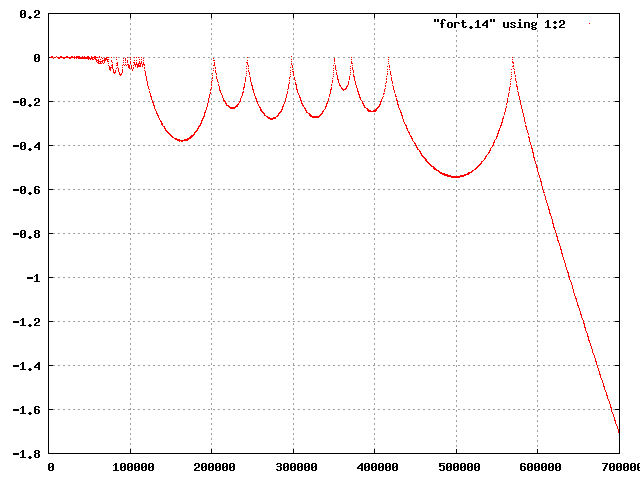 |
| 図14 factor=3,xp(3)=1.4の外側の惑星のエネルギー | 図15 factor=3,xp(3)=1.4の外側の惑星のx方向の位置の時間変化 |
図14,図15より,軌道が閉じていないときと同様に,惑星が重力圏から脱出する前に比べ,脱出した後の方が力学的エネルギーが大きくなっている.また,脱出するとき,それまでのエネルギーの極大より大きなエネルギーを得ていることがわかる.このように惑星が重力圏を脱出するとき,他の天体の力学的エネルギーをうけとって脱出する,ということがわかった.
戻る