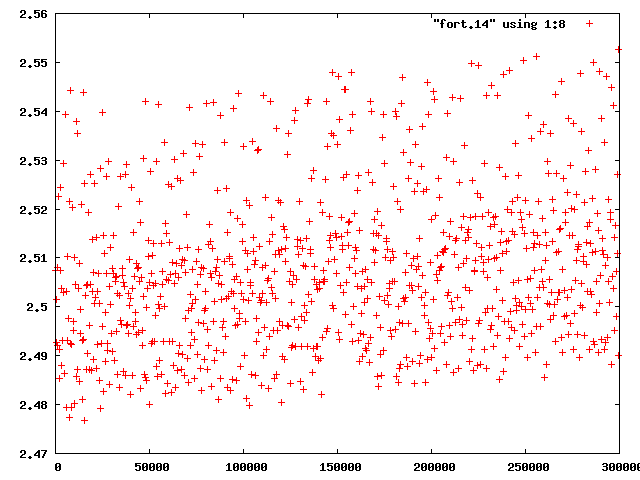
まず,楕円軌道を描く場合についてエネルギーの様子を調べた.比較的安定したfactor=2,xp(3)=1.5の場合と,軌道のばらつきがあるfactor=5,xp(3)=1.55の場合を調べ,比較した.なお図では横軸にtime,縦軸にエネルギーをとっている.
| 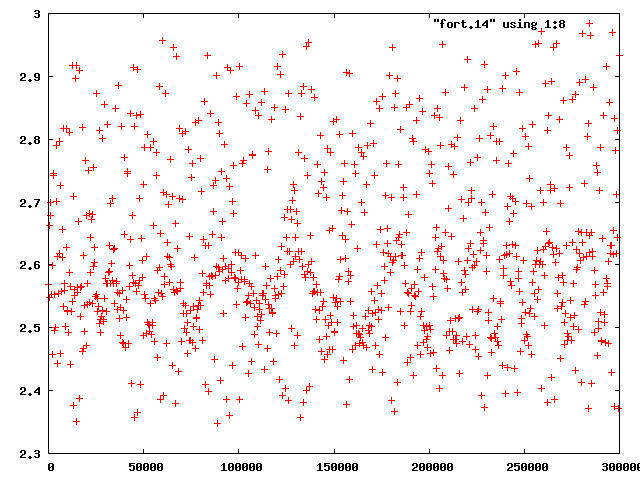 |
| 図1 factor=2,xp(3)=1.5の全エネルギー | 図2 factor=5,xp(3)=1.55の全エネルギー |
図の縦軸に注目すると,軌道が安定しているfactor=2,xp(3)=1.5の場合の方が狭い範囲に収まっていることが分かる.また,どちらもエネルギーに変動はあるものの,後で述べる不安定な場合に比べて全エネルギーの変動の幅は小さく,全エネルギーが保存されているといえる.
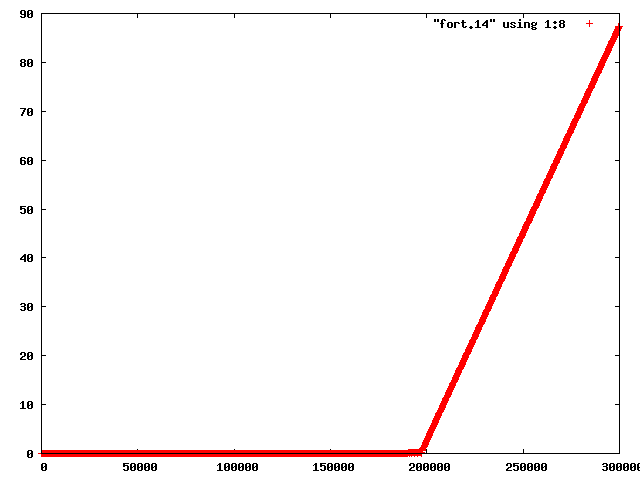
次に不安定で惑星が飛んでしまっているfactor=6,xp(3)=1.4とfactor=6,xp(3)=1.55の場合のエネルギーの様子を調べた.
| 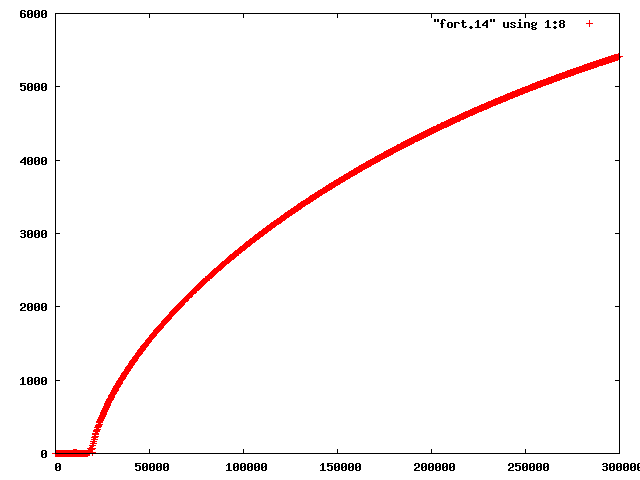 |
| 図3 factor=6,xp(3)=1.4の全エネルギー | 図4 factor=6,xp(3)=1.55の全エネルギー |
時間が経つと,あるところで急にエネルギーが増加して,エネルギー保存が成り立っていないことがわかる.これより,不安定になる原因は数値計算がうまくいっていない可能性があると考えられる.また,軌道だけでは一見して同じように見えていた二つの場合でも,エネルギーの増加の仕方が異なっているのがわかる.
全エネルギーの変化と天体の運動の関係を考えるため,factor=6,xp(3)=1.55の場合について,天体の位置のx軸方向への時間変化と中心星と内側の惑星の軌道を図5,図6に示す.
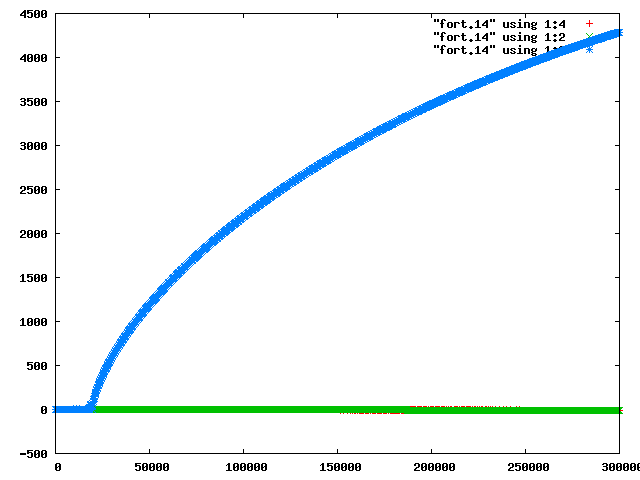
| 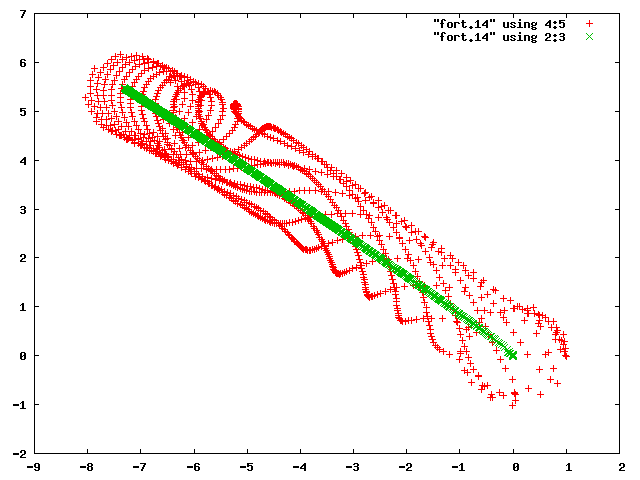 |
| 図5 factor=6,xp(3)=1.55のx方向の時間変化 | 図6 factor=6,xp(3)=1.55の外側の惑星以外の軌道 |
図4,図5より,エネルギー保存が崩れるとき,エネルギーの変動と同じように外側の惑星の位置が変化していくことが分かる.また図5からだけでは,中心星と内側の惑星の様子がわからないが,図6より,やはり二つの天体も軌道が閉じていないことがわかる.
△だったfactor=3,xp(3)=1.4の場合の全エネルギーの様子を調べた.
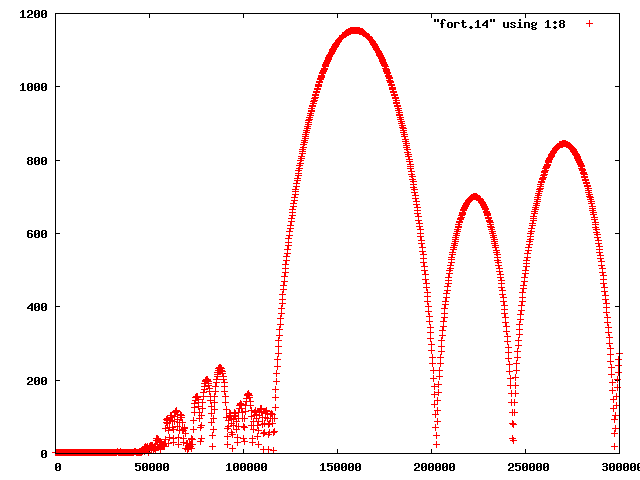 |
| 図7 factor=3,xp(3)=1.4の全エネルギー |
最初は安定だが,時間が経つにつれてエネルギーが大きく変動する様子がわかる.しかし,放物線のようにまたもとのエネルギーに戻ってきたり,放物線の振幅も,単純に時間と比例していなかったりと,微妙な状態であることがわかる.
戻る