[itbase2019]Fortran 実習 変数・配列・演算 練習問題
練習問題 1
下は, x=0.1 のときに, f(x) = x^2 (x^n は x の n 乗を表すとする) を計算する プログラムである. このプログラムを変更し, f(x) = x^5 + 6×x^4 + 2×x^3 - x^2 + 4 の値を計算するプログラム を作り, f(0.23) の値を求めなさい
program calceq implicit none real:: x real:: fx x = 0.1 fx = x**2 print *, x, fx end program calceq
答え
- 答えは, 3.988... .
練習問題 2
下は, 半径 2 m の円の円周を計算するプログラムである. これを変更して, 底面の円の半径 5.5 m, 高さ 11 cm の円筒の体積を計算するプログラムを作り, 体積を計算しなさい.
program calccircle implicit none real, parameter :: pi = 3.141592 ! 円周率 real :: radius = 2.0 ! 半径 real :: circle ! 円周 circle = 2.0 * pi * radius print *, circle end program calccircle
ヒントと答え
- 順番に少しずつ作ってみましょう.
- 高さのための変数を用意する (値を与える)
- 体積のための変数を用意する
- 単位に注意すること
- 体積を計算する
- 答えは, 10.45... m^3.
練習問題 3
数学者のラマヌジャンは円周率 (3.14159265358979323...) の近似式として下のものを見つけた.
これらを計算し, もっとも円周率の真値に近い式を見つけなさい.
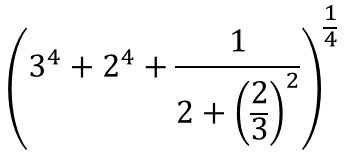
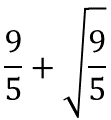
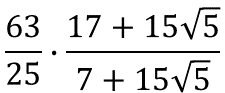
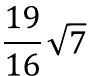
ヒントと答え
- 倍精度で計算すると良いでしょう.
- プログラムでは, 整数同士の演算の答えは整数になることに注意しましょう.
- 例えば, 2/3 の答えはいくつになるか注意しましょう.
- それぞれの式の計算結果は下のようになるだろう.
- 3.1415926525826463
- 3.1416407864998739
- 3.1415926538056880
- 3.1418296818892015
- したがって, 真値に最も近いのは 3 番目の式.
練習問題 4
温度 6000 K, 波長 0.5 μm のプランク関数の値を計算するプログラムを 作り, その値を計算しなさい. なお, プランク関数は下に示す関数である.
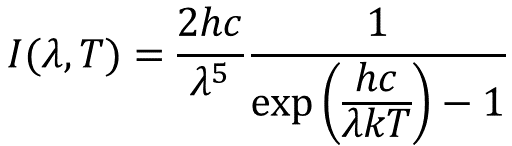
ここで, λは波長 (m), T は温度 (K), h = 6.626070040e-34 J s はプランク定数, c = 299792458 m/s は光速度, k = 1.38064852e-23 J/K はボルツマン定数である.
ヒントと答え
- 倍精度で計算すると良いでしょう / 計算しなければいけないでしょう.
- 順番に少しずつ作ってみましょう.
- プランク定数や光速度などの変数(定数)を用意する
- 波長と温度の変数を用意する
- プランク関数の値を計算する
- 単位に注意すること
- 答えは 105929.4... (W/(m**2 sr m)).
- sr は立体角の単位で, ステラジアンと呼ぶ

Keyword(s):
References:[[itbase2019]惑星学実験実習の基礎II] [[itbase2019]Fortran 実習 サブルーチンと関数 練習問題]