ここからは本格的な数値計算を行います. 処理が複雑になってくるので, irb ではなくファイルに Ruby のコードを書いたものを扱うことにします. ファイルを触る前に, 1 次元移流方程式の数値計算に関して簡単な説明を行います.
今回扱う方程式について解説します. 離散化などについては, 詳細は レクチャー編 を参照してください.
今回は 1 次元定常移流方程式を扱います. 1 次元定常移流方程式は
\[ \frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0 \]
と定義される偏微分方程式です. ここで $u$ は対象となる物理量 (たとえば温度), $t$ は時間, $x$ は空間, $c$ は移流速度であり, ここでは非ゼロの定数とします. 境界条件は 1 次元周期境界条件
\[ u(0, t) = u(L, t) \]
を用います. 初期条件は
\[ u(x, 0) = \begin{cases} 1 & \text{if $\quad L/8 \leq x \leq L/4$} \\ 0 & \text{elsewhere} \end{cases} \]
とします. この方程式の解析解は
\[ u(x, t) = u(x-ct, 0) \]
になります. すなわち, 解析解は初期に与えた波形 $u(x, 0)$ が形を変えることなく 速度 $c$ で移動することを意味します.
系の定義域を $[0, L)$ とします. 空間を $m$ 個の格子点に等分割すると, 格子の間隔は
\[ \Delta x = L / m \]
になります. また, 時間の刻み幅は $\Delta t$ とします. 上記より座標を
\[ x_j = j \Delta x \quad (j = 0, 1, ... m-1) \\ t^n = n \Delta t \quad (n = 0, 1, ...) \]
と定義します. 以降, 格子点番号に下付き添字, 時間ステップに上付き添字を用います. たとえば $u_j^n$ は $n$ ステップ目における 格子点番号 $j$ の $u$ の値を意味します.
式の離散化の方法は何種類もありますが, ここでは時間方向に一次の前進差分 (オイラー法)
\[ \left. \frac{\partial u}{\partial t} \right|_j^n = \frac{u_j^{n+1} - u_j^n}{\Delta t} \]
および空間方向に二次の中心差分
\[ \left. \frac{\partial u}{\partial x} \right|_j^n = \frac{u_{j+1}^n - u_{j-1}^n}{2 \Delta x} \]
を用いることにします. 上記を移流方程式に代入して $u_j^{n+1}$ の式として書きなおすと
\[ u_j^{n+1} = u_j^n - \frac{C_{CFL}}{2} (u_{j+1}^n - u_{j-1}^n) \]
となります. ここで
\[ C_{CFL} = \frac{c \Delta t}{\Delta x} \]
です. 上記の漸化式を用いることで $u$ の時間発展を計算することができます.
計算設定は以下を用いることにします.
\[ u(x, 0) = \begin{cases} 1 & \text{if $\quad L/8 \leq x \leq L/4$} \\ 0 & \text{elsewhere} \end{cases} \]
上記の離散化を行った方程式を解く Ruby プログラムを用意したので ダウンロードしてみましょう.
ITPASS サーバの設定の都合上, Ruby (*.rb) ファイルを そのままダウンロードさせることができないため, txt で置いています.
$ wget http://itpass.scitec.kobe-u.ac.jp/exp/fy2012/120727/practice/adv.txt $ mv adv.txt adv.rb
less などで読んでみましょう. 「メソッド定義」の部分は読み飛ばしてかまいません.
コードを読むにあたっての注意を記します. 以下はいずれも今回のサンプルコード独自のものです. 実習の時間では触る必要はありませんが, 興味があれば変更してもかまいません.
配列 u を周期境界条件で i 要素分ずらした結果を返す. u が [0, 1, 2, ..., n] の場合は u.sft(1) は [n, 0, 1, 2, ..., ,n-1] となる.
u を赤線で, 解析解を黒線の折れ線グラフとして描画するメソッド.
コードを読んで不審点に気づいた人もいるでしょうが, とりあえずこのまま実行してみます.
実行するには
$ ruby adv.rb
とするか,
$ chmod a+x adv.rb
で実行権限を与えた上で
$ ./adv.rb
とします.
すると下記のようなエラーメッセージが表示されます.
adv.rb:117: syntax error, unexpected ')'
dudx = (u.sft(1) - ??????) / ??????
^
adv.rb:126: syntax error, unexpected '\n'
adv.rb:131: syntax error, unexpected $end, expecting ')'
実は, このサンプルコードは一部が ?????? と虫食いになっているので そのままでは実行できません.
Ruby のエラーの形式は
(問題があったファイル名):(問題があった行):(エラーの内容)
となっています. そのような行が複数行連なっている場合は, エラーの発生した場所からループやメソッドなどを遡った 結果を次々と表示しています. たいていの場合は指摘された行付近にバグが潜んでいるはずです.
エラーメッセージやこれまでの実習資料の記述を参考に 修正してみましょう.
式の前に `p' をつけると 式の返り値が標準出力に出力されます. 途中経過を確認したい場合に活用しましょう.
どうしてもうまくいかない場合は 以下の回答例を参考にしてください.
ウィンドウが表示された場合は, キーボードの Enter を連打または押しっぱなしにすると 図の中の時間が進みます. うまくいかない場合はマウスでウィンドウをアクティブにしてから行ってください.
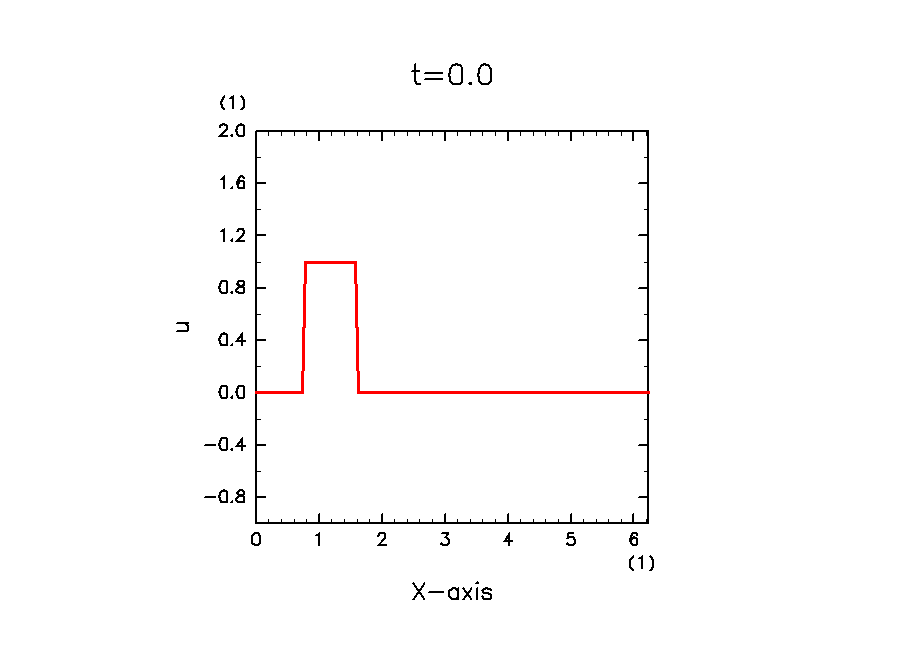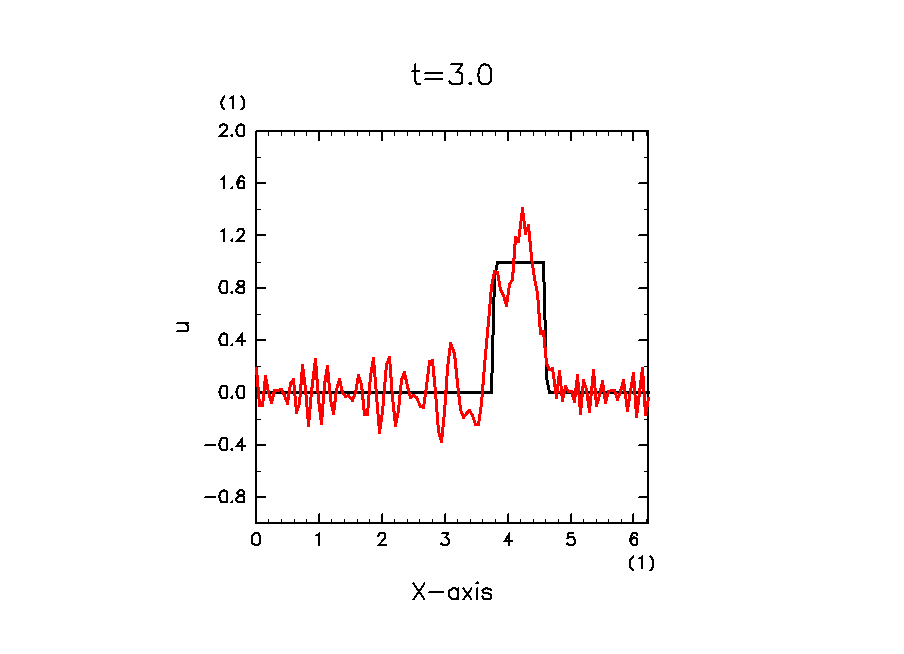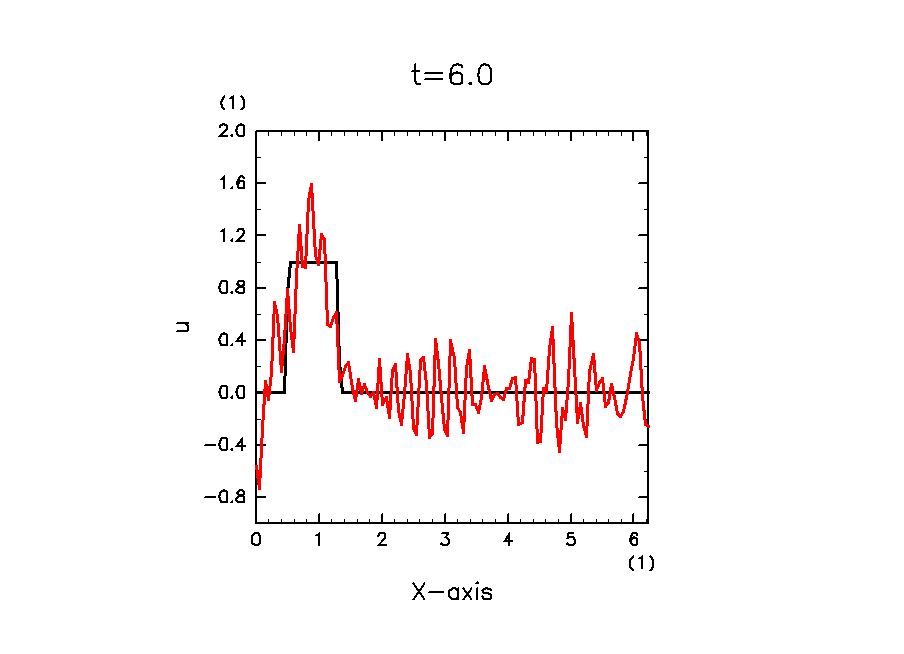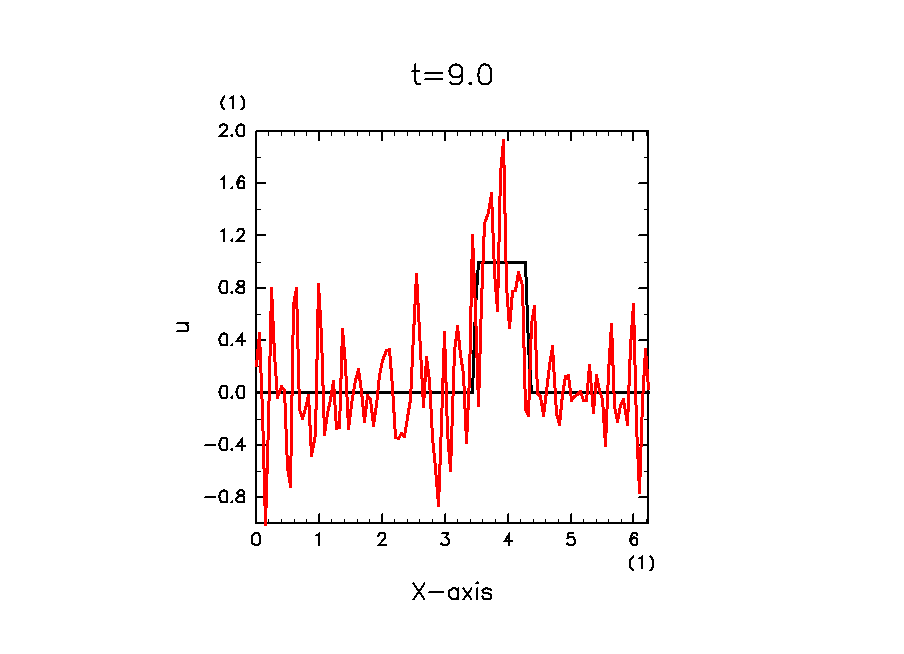
成功すれば, 以下のような絵が描画されます. 黒線が解析解, 赤線が数値解です.

移流されている雰囲気は出ていますが, 時間経過とともに高波数のノイズが成長しているのが見てとれます. なぜこのようになるかの詳細は レクチャー編 を参照してください.